Lecture notes

last updated 08.04.2025 (lectures 1-6 and 8-11), work in progress, use with caution (and do let me know about any problems and errors)

Problem sheets and tutorials

Moodle link for submitting your solutions

Problem sheet 1 (due on 8.05)
Problem sheet 2 (due on 22.05)
Problem sheet 3 (due on 12.06)
Problem sheet 4 (due on 26.06)

8.05.2025: Solutions to Problem sheet 1
15.05.2025: Applications of Ginzburg-Landau theory
22.05.2025: Solutions to Problem sheet 2
12.06.2025: Solutions to Problem sheet 3
26.06.2025: Solutions to Problem sheet 4

Lecture 9 (19.06.2025). Quantum interference

Quantum states on tap

RCSJ model, tilted washboard potential

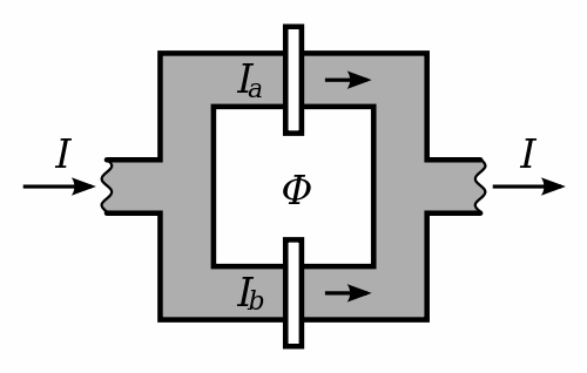
SQUID

superconducting qubits

SQUID: technical details and examples of magnetometry
Superconducting qubits: introductory reading
State of quantum computing: Building a quantum economy (economical and technological report)

Lecture 8 (12.06.2025). Josephson junctions

lecture slides

What is at the end of the tunnel?

ac and dc Josephson effects

voltage standard

Brian Josephson

The Nobel laureate versus the graduate student, or Josephson against Bardeen
History of voltage standards with instructive examples from the past

Lecture 7 (5.06.2025). The world of vortices

lecture slides

Flow, creep, and pinning: zoology of superconductors

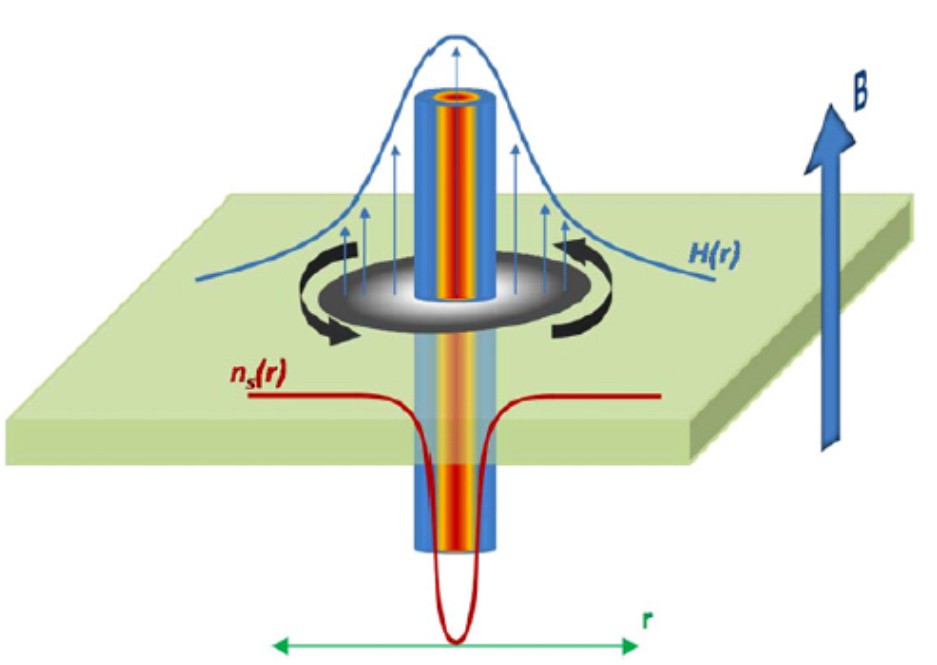
vortex lattice, pinning

small-angle neutron scattering

superconducting cables and superconducting magnets

Impressive magnet quenches: one and two
Dangerous experiments with a superconducting magnet
Quantum locking experiment, and another one
Overview of superconducting cables
Progress reports of superconducting cables: Ampacity (Essen), SuperRail (Paris)

Lecture 6 (22.05.2025). Vortices, and where is the critical field?

lecture slides

Image from Supercond. Sci. Tech. 27, 063001 (2014)

New strategy for superconductors: when type-II is better than type-I

type-II superconductors, vortices, lower and upper critical fields

Nb-based superconductors

Alexey Abrikosov

Fabrication and application challenges of Nb-based superconductors

Lecture 5 (15.05.2025). Coherence vs. penetration

lecture slides

The invisible length scales of a superconductor

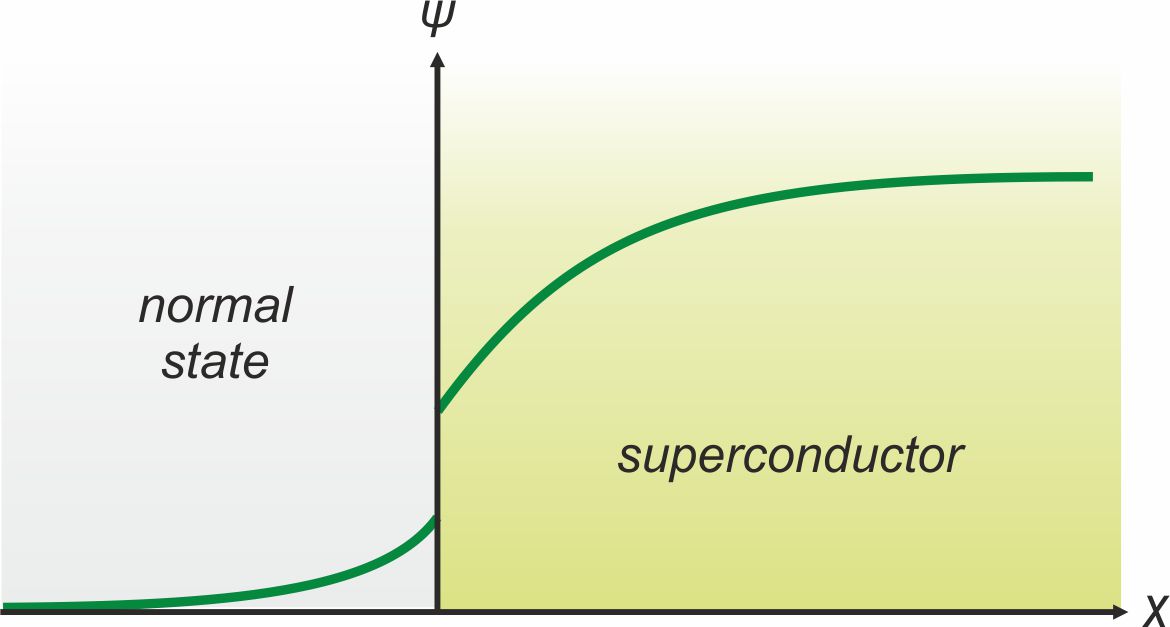
Ginzburg-Landau theory, coherence length

proximity effect

Vitaly Ginzburg

Ginzburg about his theory (his style looms through the text)
Proximity effect in superconductors as of 1968, and state of the art in 2004 (an accessible but advanced reading!)

Lecture 4 (8.05.2025). Problems at the interface

lecture slides

Things get difficult when you reach the boundary: a critical blow to London's best theory

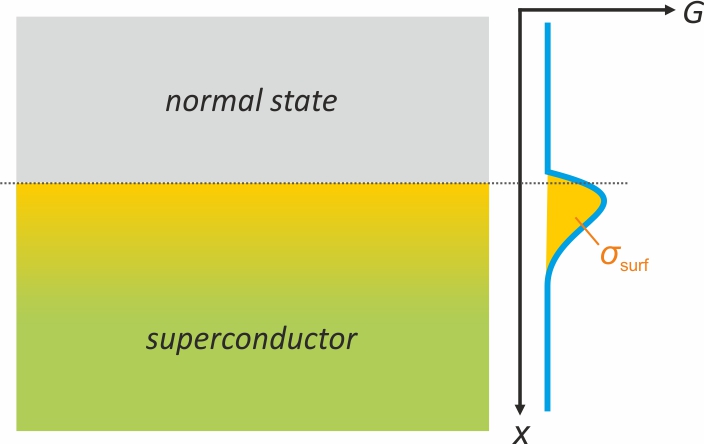
surface energy, Landau theory of phase transitions

superconducting tapes

Lev Landau

About Landau's theory minimum, seminar, and workstyle
Landau and superfluidity (and some personal history related to his arrest)
Applications of Landau theory (not a fun reading, but it gives some real-world examples)

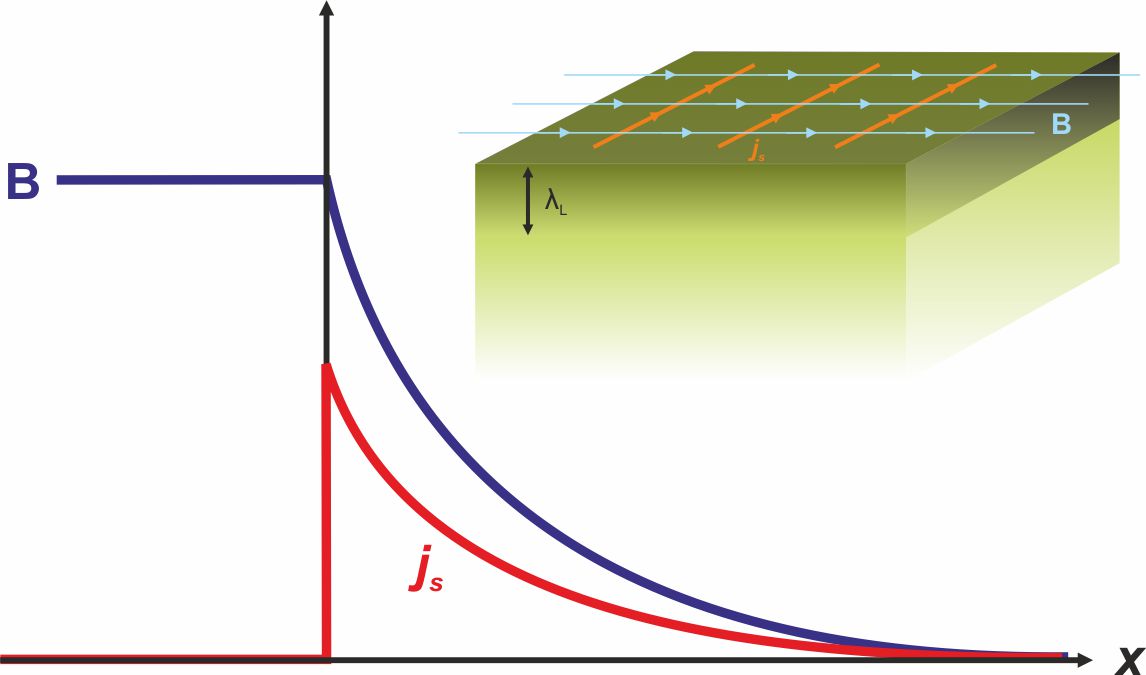
Lecture 3 (24.04.2025). How deep can field go?

lecture slides

Spatial distribution of field and supercurrent, 10 years to measure the flux

penetration depth, London theory

flux quantization

Fritz London

Thinking big, or London's work in physics-wide context

Lecture 2 (17.04.2025). Thermodynamics of superconductors

lecture slides

Photo by Julien Bobroff, Frederic Bouquet, Jeffrey Quilliam (CC-BY-SA)

Superconductor vs. magnetic field, and how they see each other

Meissner effect, demagnetization, latent heat

magnetic levitation (trains)

Paul Ehrenfest

Early history of superconductivity, or why it took 20 years to discover Meissner effect
Magnetic levitation: with and without a superconductor
Classification of phase transitions in the historical perspective, or why first order and second order is not always enough

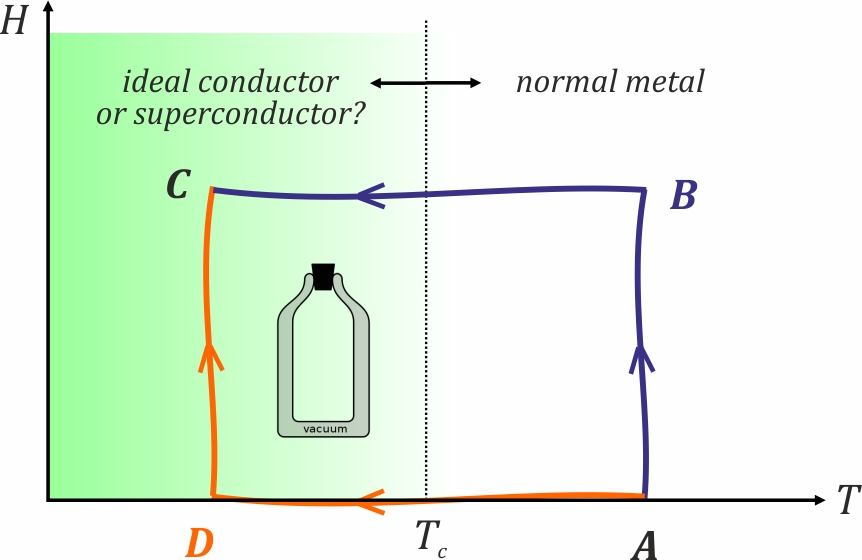
Lecture 1 (10.04.2025): Expulsion of magnetic field

lecture slides

We will learn why superconductors do not like magnetic field, and how to make things cool

ideal conductor and ideal diamagnet

cryogenics

mercury

Heike Kamerlingh Onnes

History of Kamerlingh Onnes' discovery: short version and longer version
How bad is the helium shortage situation? – Summary and detailed report
Cryogenic helium refrigeration for middle and large powers: a 700-page treatise with an exhilarated description of cryostats and liquefiers

N.B. Lecture slides contain images from publications that may be licensed differently from the rest of this webpage.